
|
ПРИМЕНЕНИЕ СТАТИСТИЧЕСКИХ МЕТОДОВ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТА ПРИ ПРОВЕДЕНИИ УЧЕБНО-ИССЛЕДОВАТЕЛЬСКИХ ЛАБОРАТОРНЫХ РАБОТ.
Учебно-исследовательская лабораторная работа состоит из следующих основных этапов:
1. подготовка к исследованию. Определяется цель и формулируются задачи исследования; разрабатывается программа и методика исследовании;
2. экспериментальное исследование. Этот этап предполагает планирование опытов, подготовку к опытам, их проведение и статистическую обработку данных;
3. анализ результатов экспериментальных исследовании. Это путь от наблюдения к аналитическому обобщению, т. е. к математическому описанию исследуемого объекта и раскрытию характера воздействия отдельных факторов на исследуемый процесс.
Рассмотрим методику планирования эксперимента и обработки опытных данных.
В результате проведения экспериментальных работ необходимо получить некоторое представление о поверхности отклика, которую в общем случае можно аналитически описан, функцией:
где з - исследуемый параметр;
Х1, Х2, … , Хк - независимые переменные (факторы), от которых зависит отклик з и которыми можно варьировать при проведении эксперимента.
Обычно исследование ведется при неполном знании механизма изучаемых явлении и вид функции (1) неизвестен, поэтому ее аппроксимируют полиномом. Модели полиномного вида удобны тем, что с их помощью любая непрерывная функция (1) может быть описана как угодно точно. Точность описания зависит от степени полинома. С увеличением степс-пи полинома повышается точность описания, однако это приводит к увеличению числа оцениваемых параметров модели и, следовательно, количества опытов, по результатам которых оценивают параметры модели.
Можно уменьшить количество опытов в эксперименте и повысить точность определения опенок параметров, выбирая условия опытов в соответствии с основными положениями теории планирования эксперимента. Планирование эксперимента - это процедура выбора числа и условий проведения опытов, необходимых и достаточных для решения поставленной задачи с требуемой точностью.
Рассмотрим основные понятия, используемые в теории планирования эксперимента.
Фактором называется измеряемая переменная величина, принимающая в некоторый момент времени определенное значение. Каждый фактор имеет область определения, т. е. совокупность всех значений, которые в принципе может принимать данный фактор. В эксперименте используется только часть значений, входящих в область определения. Каждый фактор может принимать в опыте одно из нескольких значений. Такие значения называются уровнями. Минимальное число уровней факторов, используемых при построении плана эксперимента, зависит от степени полинома. Для оценки параметров модели в виде полинома первой степени или неполного квадратичного полинома используют планы эксперимента, в которых каждый фактор варьируется на двух уровнях.
Полным факторным экспериментом (ПФЭ) называют эксперимент, в котором реализуются все возможные сочетания уровней факторов. Число опытов ПФЭ:
где р - число уровней; k - число факторов.
Дробным факторным экспериментом (ДФЭ) называют эксперимент, предусматривающий реализацию части опытов ПФЭ. Применение ДФЭ позволяет уменьшить число опытов.
Обработка результатов опытов упрощается, если от значений факторов в натуральном масштабе перейти к безразмерным переменным Хi. Для планов типа 2К переход выполняется таким образом, чтобы наибольшее значение фактора Хiв (верхний уровень) в кодированном масштабе соответствовало Xi=+1, а наименьшее значение Хiн (нижний уровень) - Xi=-1. Промежуточные значения Хi факторов в кодированном масштабе находят по формуле:
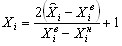 , (2) , (2)где Хi - значение i-го фактора в натуральном масштабе.
При проведении лабораторных работ, как правило, исследуется небольшая область факторного пространства, поэтому достаточной является аппроксимация неизвестной функции отклика линейной моделью:
или неполной квадратичной моделью:
где y - оценка ; bo, b1, bk, bk-1, - параметры модели, которые необходимо определить по результатам опытов.
Планы эксперимента, которые рекомендуется использовать в учебно-исследовательских лабораторных работах, приведены в приложении 2. В таблицах верхний уровень обозначен «+», а нижний - «-». Точность определения параметров модели повышается, если каждый опыт, предусмотренный планом эксперимента, повторяется m раз. Обычно каждый опыт дублируют 2-3 раза, т.е. т = 2 или 3. Целесообразно количество параллельных опытов в каждой строке матрицы планирования проводить одинаковое. Это упрощает последующую обработку данных.
Обработка результатов при одинаковом числе параллельных опытов Yi и производится следующим образом:
 ; u = 1, 2, … , m; j = 1, 2, … , N, (5) ; u = 1, 2, … , m; j = 1, 2, … , N, (5)где yju - значение функции отклика в u-ом параллельном опыте;
j - номер опыта в матрице планирования;
N - число опытов в матрице планирования.
2. определяют оценку дисперсии опыта:
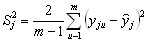 , (6) , (6)3. проверяют гипотезу однородности дисперсии по G-критерию Кохрена:
 , (7) , (7)Если полученное значение критерия не превышает табличного, то гипотеза однородности дисперсий не отвергается;
4. если дисперсии однородны, то находят дисперсию воспроизводимости эксперимента:
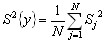 , (8) , (8) Дисперсия
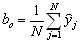 , (9) , (9)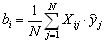 , (10) , (10)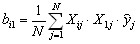 , (11) , (11)где Xij, X1j - кодированные значения i-го и 1-го факторов в j-м опыте. Для планов, приведенных в приложении 2, эти значения равны ± 1;
5. находят дисперсию коэффициентов регрессии. Для рассматриваемых планов дисперсии всех коэффициентов, равны:
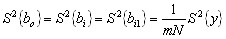 , (12) , (12)6. проверяют значимость коэффициентов регрессии, сопоставляя их значения с доверительным интервалом. Доверительные интервалы находят по формулам:
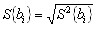 , (13) , (13)где t - значение t-критерия для принятого уровня значимости и числа степеней свободы, с которым определена дисперсия s2{y}:
Коэффициент значим, если его абсолютная величина больше доверительного интервала. Незначимые коэффициенты могут быть исключены из модели.
7. проверяют гипотезу адекватности полученной модели результатом эксперимента. Для этого находят дисперсию:
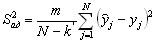 , (14) , (14)где k' - число значимых коэффициентов в модели;
уj - значение функции отклика, вычисленное по полученной модели для условий j-го опыта.
Однородность дисперсий S2ад и S2{y} проверяют с помощью F-критерия, сопоставляя расчетное значение критерия с табличным:
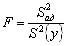 . (15) . (15)Гипотеза адекватности не отвергается, если полученное значение критерия меньше табличного, определенного для принятого уровня значимости и чисел степеней свободы, с которыми найдены дисперсии S2ад и s2{y}.
Адекватная модель может быть использована для дальнейших исследований. В случае неадекватности модели можно перейти к полиномной модели более высокого порядка или сузить область эксперимента.
Для перехода от кодированных значений факторов Xi, к значениям факторов в натуральном масштабе Xi необходимо в полученную модель подставить вместо Xi их выражения из (2) и произвести преобразования.
В технологии машиностроения часто зависимость исследуемой величины от основных факторов процесса описывают уравнением вида:
где С - коэффициент; a1, a2 , …, aк - показатели степени.
Логарифмированием уравнение (16) можно привести к линейной модели (3), а для оценки параметров полученной модели использовать описанные выше планы. Переход от натуральных значений факторов к их значениям в кодированном масштабе осуществляется по формуле:
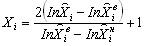 . (18) . (18)Обработка данных производится в соответствии с изложенной выше методикой. После подстановки в полученную линейную модель вместо значений факторов в кодированном масштабе выражений (17) и преобразований потенцированием получают модель вида (16).
ПРИЛОЖЕНИЕ 2
ПЛАНЫ ЭКСПЕРИМЕНТА, РЕКОМЕНДУЕМЫЕ ДЛЯ ИСПОЛЬЗОВАНИЯ ПРИ ПРОВЕДЕНИИ УЧЕБНО-ИССЛЕДОВАТЕЛЬСКИХ ЛАБОРАТОРНЫХ РАБОТ.
Таблица П. 2.1
ПЛАН ДЛЯ К=2
Таблица П. 2.2
ПЛАН ДЛЯ К = 3
Таблица П. 2.3
ПЛАН ДЛЯ K = 4
Таблица П. 2.4
ПЛАН ДЛЯ K = 4
ПРИЛОЖЕНИЕ 3
ПРИМЕРЫ ОБРАБОТКИ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ ПРИ ИСПОЛЬЗОВАНИИ ПФЭ.
Пример 1.
Необходимо описать зависимость стойкости концевых фрез от заднего угла a, переднего угла g - ширины ленточки f, уровни факторов указаны в таблице П. 3.1.
Таблица П. 3.1
Уровни факторов.
Матрица планирования, условия и результаты опытов приведены в таблице П. 3.2. Каждый опыт, предусмотренный матрицей планирования, повторяли три раза, т.е. т = 3. Использовали ПФЭ типа 23.
Обработку данных выполнили следующим образом:
1. по формуле (5) приложения 1 нашли средние значения стойкости в каждом опыте матрицы планирования. В первом опыте среднее значение:
y1= (30,75 + 29,50 + 38,15) =32,80.
Аналогично определили средние значения yj в других опытах.
2. по формуле (6) определили дисперсии опытов, например, в первом опыте:
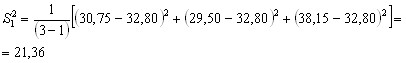 Полученные значения Sj2 для других опытов указаны в таблице П. 3.2.
Таблица П. 3.2.
Матрица планирования, условия и результатов опытов.
3. для проверки гипотезы однородности дисперсий вычислили отношение максимальной дисперсии s2j max = 55,44 к сумме дисперсий, которая оказалась равной Уs2j = 249,00.
G = 55,44/249,00 = 0,2226.
Табличное значение критерия при 5%-ном уровне значимости GT = 0,5157. Полученное значение критерия меньше табличного, поэтому гипотеза однородности дисперсий не отвергается.
4. нашли дисперсию воспроизводимости эксперимента по формуле (8):
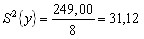 . .5. нашли параметры bo, b1, bk, bk-1 неполного квадратичного полинома по формулам (9) - (11):
b0= (1/8)(32,80 + 25,62 + 30,72 + 18,1 1 + 52,62 + 34,83 + 44,07 + 36,90) = 34,46;
b1=(1/8)(32,80 - 25,62 + 30,72 - 18,11 + 52,62 - 34,83 + 44,07 - 12,60) = -5,59.
Аналогично определили значения остальных коэффициентов регрессии:
b2=2,01; b1 = 7,64; b12 = 0,65; b13=0,65; b23 = 0,39.
6. дисперсии коэффициентов регрессии, вычисленные по формуле (12):
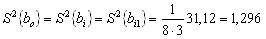 , , 6. для проверки значимости коэффициентов регрессии нашли доверительный интервал. Табличное значение t-критерия для 5%-го уровня значимости и числа степеней 8(3- 1) = 16 равно 2,12:
Коэффициенты b12, b13, b23 меньше доверительного интервала по абсолютной величине, поэтому их можно признать статистически незначимыми и исключить из уравнения регрессии.
После исключения незначимых коэффициентов регрессии получили модель в кодированных переменных:
y=34,46 + 5,59x1 + 2,01x2 - 7,64x3;
7. для проверки гипотезы адекватности полученной модели необходимо оценить отклонение стойкости, предсказанное моделью yj, от экспериментальных значений yj. Значения yj находили, подставляя вместо х1, х2 и x3 их значения из матрицы планирования, например, для первого опыта x1= +l; х2 = +1; x3 = + 1, тогда
у1 = 34,46 + 5,59 + 2,01 - 7,64 = 34,5.
Для второго опыта х1 = - 1; х2= + 1; x3 = + 1, следовательно,
y2 = 34,46 - 5,59 + 2,01 - 7,64 = 23,3.
Значения уi для других опытов приведены в таблице П. 3.2. По формуле (14):
S2 ад = (32,80 - 34,5)2 + (25,62 - 23,3)2 + (30,72 - 30,4)2 + (18,11 - 19,2)2 + (52,62 - 50,0)2 + (34,83 - 38,6)2 + (44,07 - 45,7)2 + (36,90 - 34,5)2 = 29,2.
В нашем случае s2aд < s2{y}, (29,2 < 31,12), поэтому гипотезу адекватности модели можно принять без расчета критерия Фишера.
Чтобы получить модель в натуральных переменных a, g и f, необходимо вместо X1, X2, X3 подставить выражения:
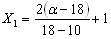 , , 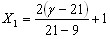 , , 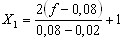 . .Формулы преобразования получены путем подстановки верхних и нижних уровней факторов в выражение (2) приложение 1.
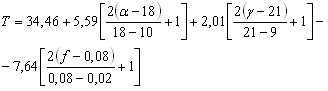 Пример 2.
Математическая модель процесса представлена уравнением степенного вида. Исследован процесс хонингования отверстий. Требуется установить влияние окружной скорости Vo хона, скорости Vп, его возвратно-поступательного движения и давления Ру на шероховатость поверхности.
Сделано предположение, что зависимость шероховатости Ra поверхности от исследуемых факторов можно представить уравнением регрессии степенного вида:
Уравнение после потенцирования примет вид:
Уровни факторов, принятые в исследовании, приведены в таблицы П. 3.3.
Таблица П. 3.3
Уровни факторов.
В качестве матрицы планирования использовали ПФЭ типа 23. Опыты не дублировали.
Расчет коэффициентов регрессии выполняли аналогично примеру 1. Получены следующие значения: b0 = 0,2925; b1 = - 0,16125; b2= - 0,1775;
bз = 0,15175; b12 = - 0,06275; b13 = - 0,039; b23 = 0,02025.
Так как опыты, предусмотренные матрицей планирования, не дублировали, то для нахождения дисперсии воспроизводимости эксперимента провели дополнительно четыре опыта. Дисперсия s2{y} = 0,007522. Дисперсия коэффициентов уравнения регрессии s2{bi} = 0,00094. Доверительный интервал коэффициентов.
Таблица П. 3.4
Матрица планирования, условия и результаты опытов.
Коэффициенты b12, b3, b23 по абсолютной величине меньше доверительного интервала, поэтому их можно считать статистически незначимыми и исключить из уравнения регрессии. После исключения статистически незначимых коэффициентов уравнение регрессии примет вид:
y = 0,2925 - 0,16125џX1 - 0,1775џX2 + 0,15175џX3.
Проверка показала, что гипотеза адекватности модели не отвергается, так как табличное значение F-критерия больше расчетного.
Для перехода от кодированных значений факторов к их значениям в натуральном масштабе использовали формулу (17), приложение 1:
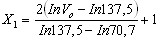 , (18) , (18)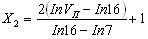 , (19) , (19)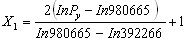 . (20) . (20)Подставив вместо X1, X2, X3 их выражения из формул (18) - (20), получили:
 После преобразования получили:
Потенцируя полученное выражение, находим зависимость шероховатости поверхности от исследуемых факторов процесса хонингования:
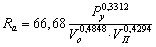 . . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
© 2009 "Режущий инструмент". При копировании ссылка обязательна !!!
|